2015-07-01 breedR version: 0.10.8
Douglas dataset
Description of Douglas dataset
data("douglas")
str(douglas)
'data.frame': 9630 obs. of 15 variables: $ self : num 135 136 137 138 139 140 141 142 143 144 ... $ dad : num 41 41 41 41 41 41 41 41 41 41 ... $ mum : num 21 21 21 21 21 21 21 21 21 21 ... $ orig : Factor w/ 11 levels "pA","pB","pC",..: 1 1 1 1 1 1 1 1 1 1 ... $ site : Factor w/ 3 levels "s1","s2","s3": 1 1 1 1 1 1 1 1 1 1 ... $ block: Factor w/ 127 levels "s1:1","s1:2",..: 11 44 24 28 13 35 8 40 3 15 ... $ x : num 6 27 45 57 57 60 63 66 66 75 ... $ y : num 81 135 90 45 327 474 450 21 234 483 ... $ H02 : int NA NA NA NA NA NA NA NA NA NA ... $ H03 : int NA NA NA NA NA NA NA NA NA NA ... $ H04 : int NA NA NA NA NA NA NA NA NA NA ... $ H05 : int 634 581 611 370 721 488 574 498 528 620 ... $ C13 : int 586 474 715 372 665 558 490 372 527 612 ... $ AN : Factor w/ 5 levels "1","2","3","4",..: NA NA NA NA NA NA NA NA NA NA ... $ BR : Factor w/ 5 levels "1","2","3","4",..: NA NA NA NA NA NA NA NA NA NA ...
Origins by site
with(douglas, table(orig, site))
site orig s1 s2 s3 pA 1381 1326 635 pB 870 815 111 pC 930 1030 80 pD 28 1 0 pE 265 0 0 pF 502 673 388 pG 0 116 26 pH 0 78 54 pI 0 78 52 pJ 0 78 55 pK 0 0 58
Spatial arrangement
ggplot(douglas, aes(x, y, color = block)) + geom_point(show_guide = FALSE) + facet_wrap(~ site)
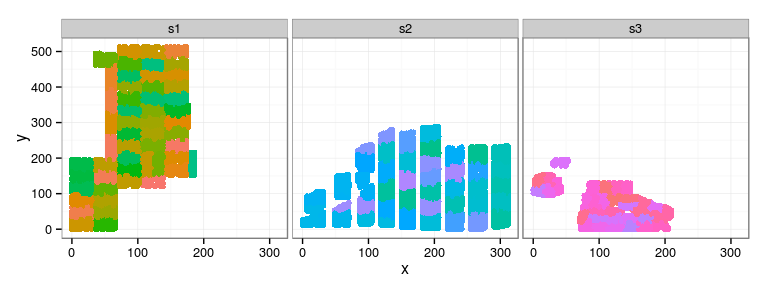
Model fit
Statistical model
Excercise: write the following model in breedR:
\[ \begin{aligned} \mathrm{CR13} = & \mathrm{site} + \mathrm{orig} + fam + bl_\mathrm{site} + fsi + \varepsilon\\ fam \sim & \mathcal{N}(0, \sigma_f^2) \\ bl_s \sim & \mathcal{N}(0, \sigma_{b(s)}^2), \quad s = 1, 2, 3 \\ fsi \sim & \mathcal{N}(0, \sigma_{i}^2) \\ \varepsilon \sim & \mathcal{N}(0, \sigma^2) \end{aligned} \]
- Adjust for blocks within each site
- (possibly with different variabilities)
Preparation of dataset
## create site-wise block variables (i.e. bl_i = bl * Ind(i)) dat <- transform(douglas, bl1 = block, bl2 = block, bl3 = block) dat$bl1[dat$site != "s1"] <- NA dat$bl2[dat$site != "s2"] <- NA dat$bl3[dat$site != "s3"] <- NA dat <- droplevels(dat) ## variable family (taken as a maternal effect) dat$fam <- factor(dat$mum) ## family-site interaction variable dat <- transform(dat, famxsite = factor(fam:site))
Basic Family-Site interaction model
Model with origin and site as fixed effects, and family, blocks and family-site interaction as random effects
reml.tree <- remlf90(fixed = C13 ~ site + orig,
random = ~ fam + bl1 + bl2 + bl3 + famxsite,
data = dat, method = 'ai')
Model summary
Linear Mixed Model with pedigree and spatial effects fit by AI-REMLF90 ver. 1.110
Data: dat
AIC BIC logLik
109427 109470 -54708
Parameters of special components:
Variance components:
Estimated variances S.E.
fam 1339.70 235.07
bl1 736.37 182.76
bl2 66.46 50.84
bl3 1233.80 385.47
famxsite 118.43 61.54
Residual 13653.00 211.56
Fixed effects:
value s.e.
site.s1 503.4873 7.4887
site.s2 550.2785 6.7923
site.s3 474.9609 9.6581
orig.pA -8.9503 4.4835
orig.pB 0.0000 0.0000
orig.pC -42.4425 9.4899
orig.pD 52.2017 44.8236
orig.pE -26.2352 18.7055
orig.pF -37.0728 11.3151
orig.pG -47.1587 23.2942
orig.pH -14.7085 26.4218
orig.pI -49.8486 29.8747
orig.pJ -57.2313 26.3383
orig.pK -53.7943 28.7336
Minimal model diagnosis
Excercise: produce the following plots:
- histogram of residuals
- fitted vs. observations
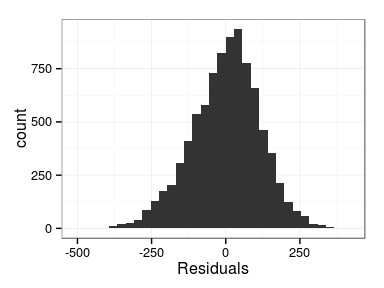
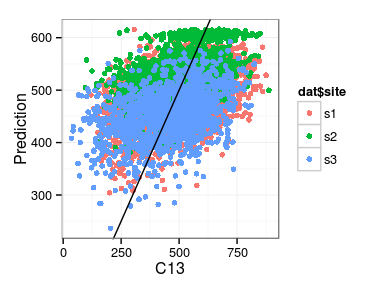
Derivation of results
Type-B correlation
reml.tree$var
Estimated variances S.E. fam 1339.700 235.070 bl1 736.370 182.760 bl2 66.463 50.844 bl3 1233.800 385.470 famxsite 118.430 61.543 Residual 13653.000 211.560
with(reml.tree,
var['fam', 1] / (var['fam', 1] + var['famxsite', 1])) %>%
round(2)
[1] 0.92
Interaction effect
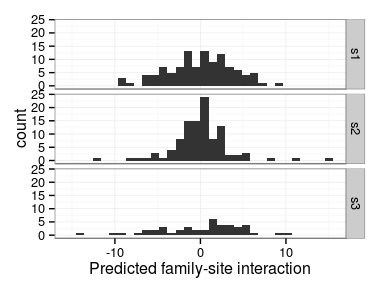
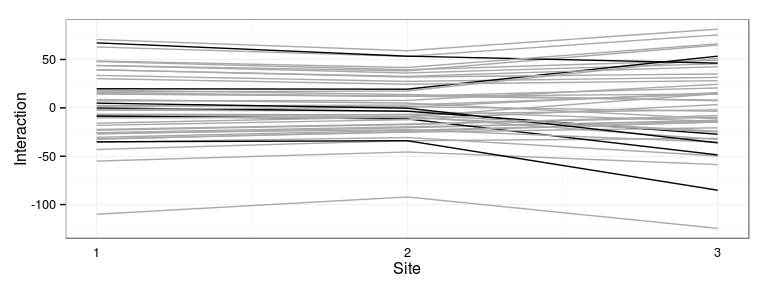
Excercise: produce the following interaction plot:
- predicted family-site interaction by site
- connect values for the same family with a line
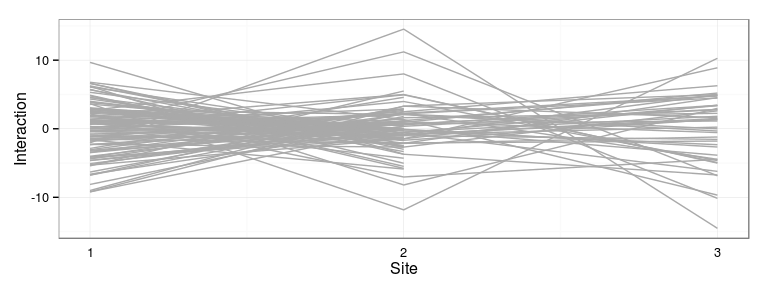
Ecovalence
Consider only families present in all the 3 sites
famxsite.tbl <- table(dat$fam, dat$site) fam3.idx <- apply(famxsite.tbl, 1, function(x) all(x>0)) table(fam3.idx)
fam3.idx FALSE TRUE 64 45
Compute ecovalence by family
Sum of squares by family (across sites) divided by total sum of squares
- (a bit of data-wrangling using
dplyr)
(dat.ecov <-
dat.fsi %>%
group_by(fam) %>%
summarise(ssfam =
sum(pred_fsi**2)) %>%
filter(fam3.idx) %>%
mutate(fratio = ssfam / sum(ssfam)))
## Check
stopifnot(
all.equal(sum(dat.ecov$fratio), 1)
)
Source: local data frame [45 x 3] fam ssfam fratio 1 1 18.447072 0.006589986 2 2 8.286972 0.002960417 3 3 58.993908 0.021074836 4 4 109.377567 0.039073769 5 5 4.886922 0.001745792 6 7 20.096726 0.007179304 7 8 33.322147 0.011903920 8 9 10.683869 0.003816679 9 10 18.413615 0.006578034 10 11 67.250109 0.024024261 .. ... ... ...
Determine most interactive families
threshold <- 0.05 dat.ecov$hi <- dat.ecov$fratio > threshold ggplot(dat.ecov, aes(fratio, fill = hi)) + geom_histogram(show_guide = FALSE)
Most interactive families: 24 28 38 48 105 106
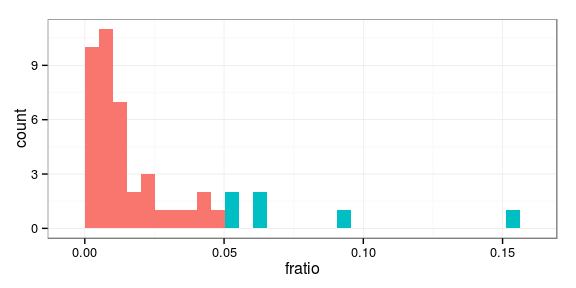
Plot most interactive families
Represent the families which interact the most with the sites:
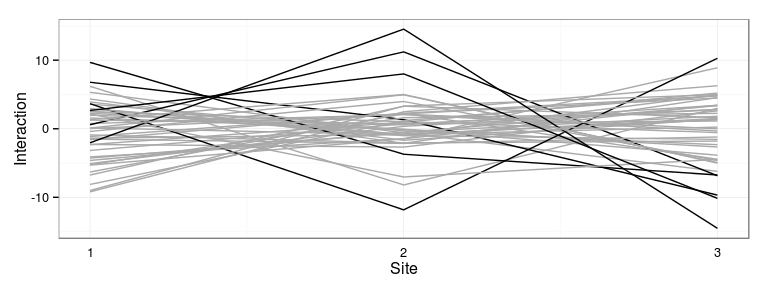
Correlations of genetic effects across sites
Compute total genetic value
The predicted genetic effect is the sum of the family effect and the family-site interaction (Excercise).
Reshape data
## reshape the genetic values ## by family (dat.gen <- dat.fsi %>% select(fam, site, pred_gen) %>% tidyr::spread(site, pred_gen) %>% tbl_df() )
Source: local data frame [109 x 4] fam s1 s2 s3 1 1 0.7708066 4.629670 6.755107 2 2 -54.7085993 -55.876654 -55.599421 3 3 -27.5767262 -17.541736 -19.202094 4 4 18.6370661 22.462160 32.831870 5 5 -9.5945562 -9.072929 -6.714122 6 6 -36.1778425 -31.010280 NA 7 7 44.9607625 39.364452 42.434652 8 8 41.1998076 44.446619 48.712357 9 9 40.6242870 36.905050 39.053858 10 10 14.6311835 10.742742 8.711473 .. ... ... ... ...
Compute correlations
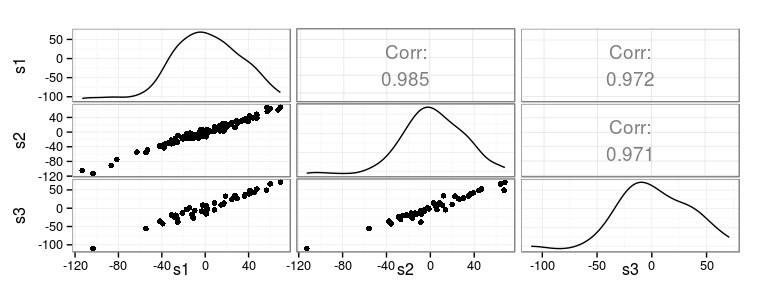
Rank correlations
Kendall (top) and Spearman (bottom)
s1 s2 s3 s1 1.000 0.875 0.834 s2 0.970 1.000 0.851 s3 0.951 0.959 1.000
Prototype zone
site-specific interaction variance?
- The model forced one single variance for the three sites.
- Should we allow different variances?
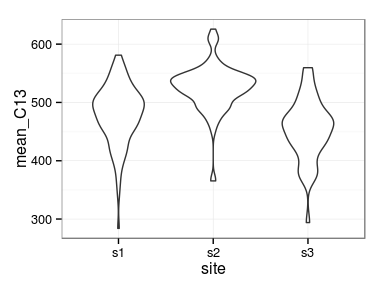
Statistical model
- Independent site-wise family effects
- Analogous to the blocks effects
\[ \begin{aligned} \mathrm{CR13} = & \mathrm{site} + \mathrm{orig} + fam + bl_\mathrm{site} + f_\mathrm{site} + \varepsilon\\ fam \sim & \mathcal{N}(0, \sigma_f^2) \\ bl_s \sim & \mathcal{N}(0, \sigma_{b(s)}^2), \quad s = 1, 2, 3 \\ f_s \sim & \mathcal{N}(0, \sigma_{f(s)}^2), \quad s = 1, 2, 3 \\ \varepsilon \sim & \mathcal{N}(0, \sigma^2) \end{aligned} \]
Model summary
Things improve a bit wrt the previous model with a single variance. It seems that in site 2 there is not much variation, nor from blocks or for GxE.
Linear Mixed Model with pedigree and spatial effects fit by REMLF90 ver. 1.78
Data: dat
AIC BIC logLik
109421 unknown -54703
Parameters of special components:
Variance components:
Estimated variances
fam 1323.000
bl1 738.100
bl2 66.610
bl3 1237.000
f1 93.980
f2 5.789
f3 662.900
Residual 13630.000
Fixed effects:
value s.e.
site.s1 503.3411 7.4347
site.s2 549.4791 6.6367
site.s3 474.4960 10.2681
orig.pA -8.6398 4.4893
orig.pB 0.0000 0.0000
orig.pC -42.1887 9.3639
orig.pD 52.3152 44.3471
orig.pE -25.6809 18.4917
orig.pF -37.6245 11.2208
orig.pG -37.9558 22.4106
orig.pH 10.1126 25.9501
orig.pI -40.8323 29.5035
orig.pJ -48.0630 26.0029
orig.pK -49.6943 36.9587
Minimal model diagnosis
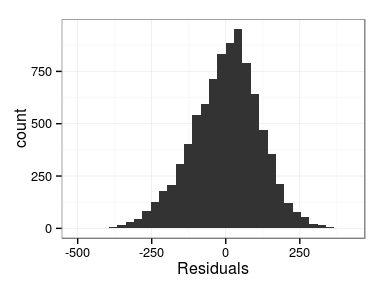
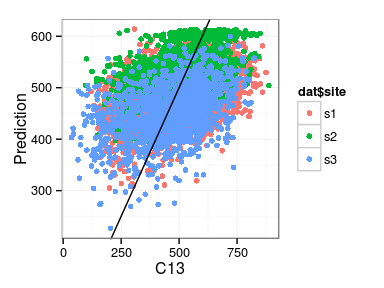
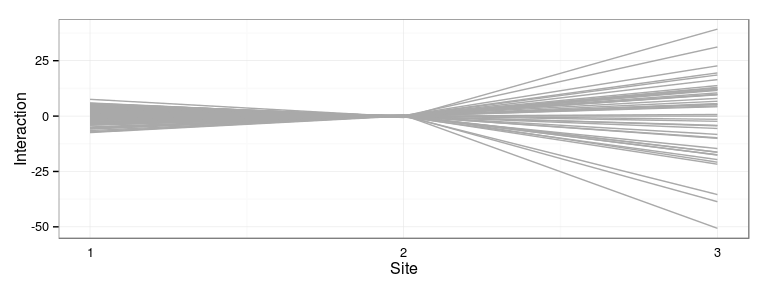
Predicted interaction effects
Differences in model predictions
- Main family and interaction effects
- Independent interactions model vs. Single interaction effect
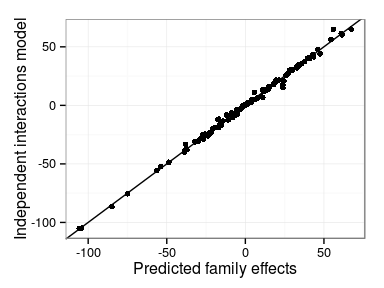
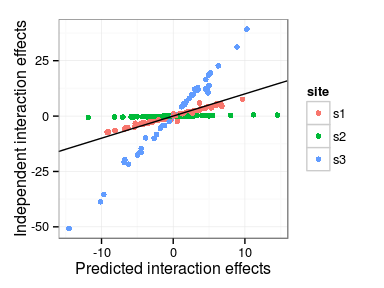
Correlations
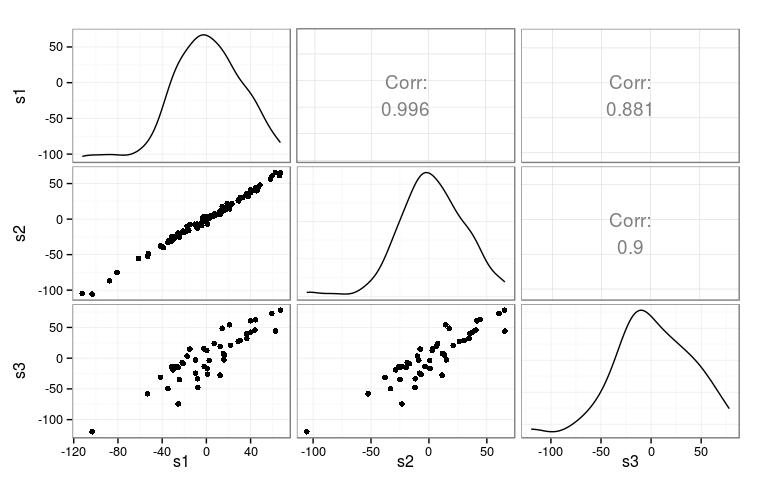
Full genetic effect
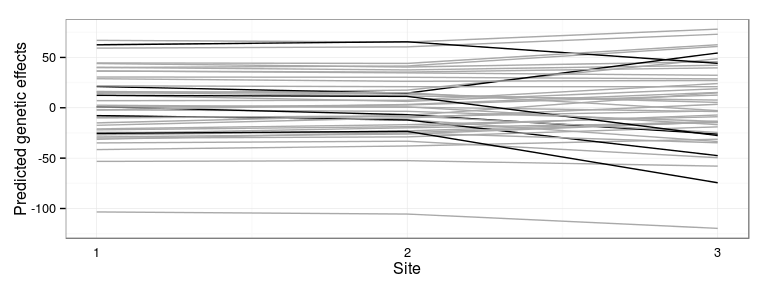
Correlated effects
Statistical model
The most effective way is to introduce the (expected) correlation between interaction effects across sites into a model parameter.
Among other things, this allows us to predict the genetic value of a family in a site where it was not observed.
\[ \begin{aligned} \mathrm{CR13} = & \mathrm{site} + \mathrm{orig} + fam + bl_\mathrm{site} + fsi + \varepsilon\\ fam \sim & \mathcal{N}(0, \sigma_f^2) \\ bl_s \sim & \mathcal{N}(0, \sigma_{b(s)}^2), \quad s = 1, 2, 3 \\ fsi = \begin{pmatrix} f_1 \\ f_2 \\ f_3 \end{pmatrix} \sim & \mathcal{N}(0, \Sigma_i \otimes \mathrm{I}) \\ \varepsilon \sim & \mathcal{N}(0, \sigma^2) \end{aligned} \]
Model summary
Linear Mixed Model with pedigree and spatial effects fit by REMLF90 ver. 1.78
Data: dat
AIC BIC logLik
109022 unknown -54500
Parameters of special components:
Variance components:
$fam
[1] 74.67
$bl1
[1] 737.6
$bl2
[1] 67.36
$bl3
[1] 1238
$fsi
f1 f2 f3
f1 1538 1239 1480
f2 1239 1009 1277
f3 1480 1277 2194
$Residual
[1] 13630
Fixed effects:
value s.e.
site.s1 464.26362 10.1012
site.s2 510.67612 9.1863
site.s3 435.08511 12.1330
orig.pA 30.80217 10.8268
orig.pB 38.62992 10.9585
orig.pC -3.97525 11.3365
orig.pD 91.39946 46.9925
orig.pE 21.13727 20.4114
orig.pF 0.00000 0.0000
orig.pG 10.58885 21.5913
orig.pH 59.81861 24.5012
orig.pI 6.00987 27.6507
orig.pJ 0.37163 24.6342
orig.pK -3.75109 38.3734
[,1] [,2] [,3] [1,] 1.00 0.99 0.81 [2,] 0.99 1.00 0.86 [3,] 0.81 0.86 1.00
Minimal model diagnosis
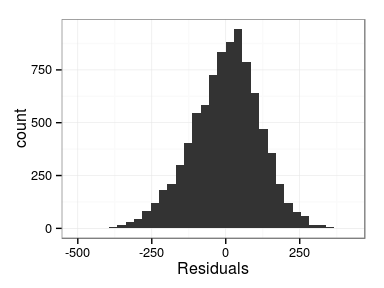
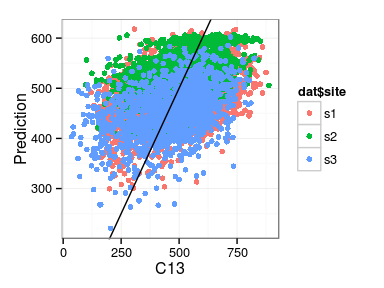
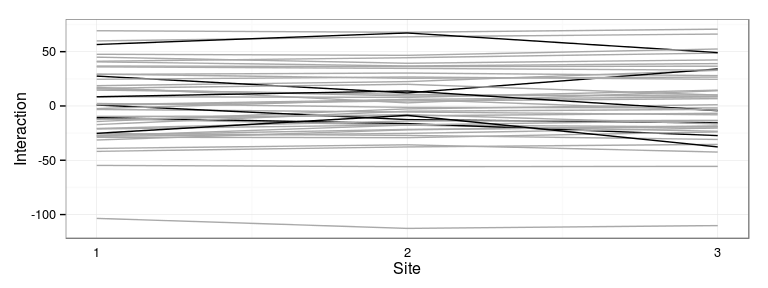
Predicted interaction effects
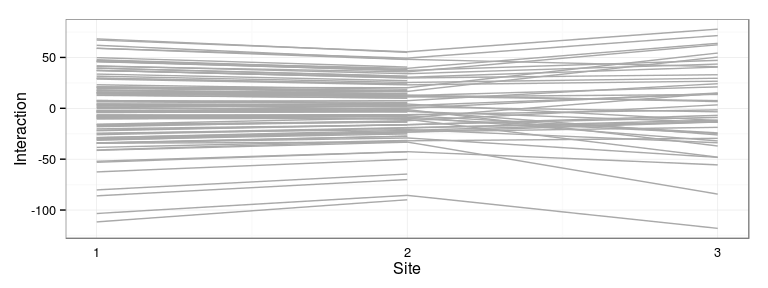
Differences in predictions
- Main family and interaction effects
- Correlated interactions model vs. Single interaction effect
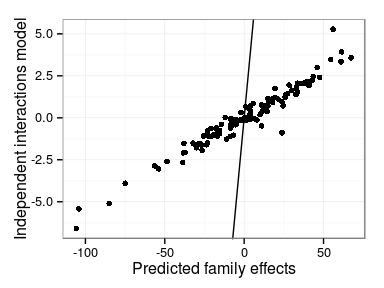
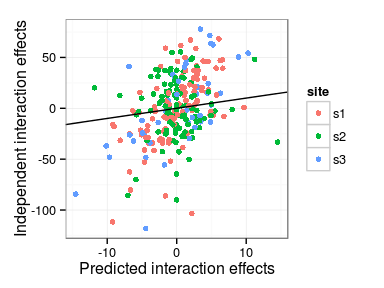
Correlations
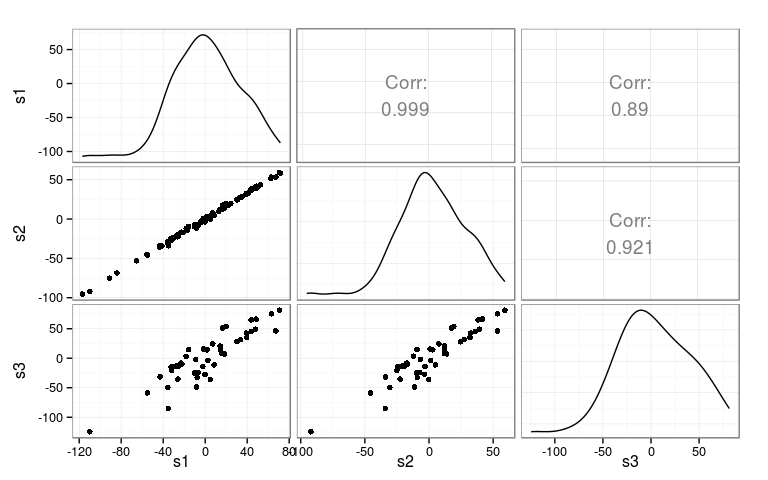
Full genetic effect
- i.e. sum of main and interaction effects
- by family and site
Spatial splines model on each site
Model hack
## Use breedR internal functions to compute splines models on each site
sp1 <- breedR:::breedr_splines(dat[dat$site == 's1', c('x', 'y')])
sp2 <- breedR:::breedr_splines(dat[dat$site == 's2' & !is.na(dat$x) & !is.na(dat$y), c('x', 'y')])
sp3 <- breedR:::breedr_splines(dat[dat$site == 's3', c('x', 'y')])
## Manually build the full incidence matrices with 0
## and the values computed before
mm1 <- model.matrix(sp1)
inc.sp1 <- Matrix::Matrix(0, nrow = nrow(dat), ncol = ncol(mm1))
inc.sp1[dat$site == 's1', ] <- mm1
mm2 <- model.matrix(sp2)
inc.sp2 <- Matrix::Matrix(0, nrow = nrow(dat), ncol = ncol(mm2))
inc.sp2[dat$site == 's2' & !is.na(dat$x) & !is.na(dat$y), ] <- mm2
mm3 <- model.matrix(sp3)
inc.sp3 <- Matrix::Matrix(0, nrow = nrow(dat), ncol = ncol(mm3))
inc.sp3[dat$site == 's3', ] <- mm3
reml.spl <- remlf90(fixed = C13 ~ site + orig,
random = ~ fam + famxsite,
generic = list(sp1 = list(inc.sp1,
breedR:::get_structure(sp1)),
sp2 = list(inc.sp2,
breedR:::get_structure(sp2)),
sp3 = list(inc.sp3,
breedR:::get_structure(sp3))),
data = dat,
method = 'em')
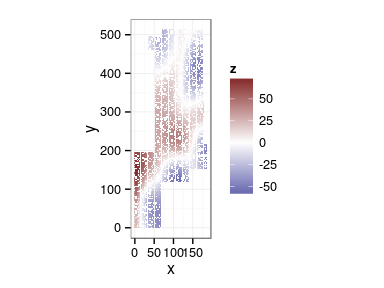
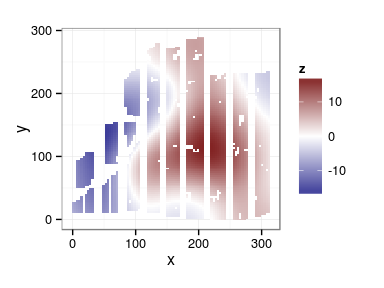
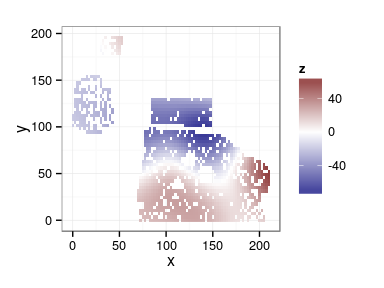
Spatial effects by site