July 1, 2015
Expoloratory Data Analysis
Number of observations
rep yr 1 2 7 4 104 110 92 5 104 110 92 7 104 110 92 8 102 110 91 10 104 110 93 11 103 110 92 13 100 110 91 14 105 110 93 15 105 110 93
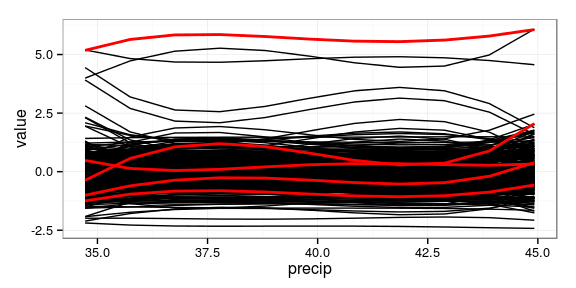
Ring-length by Mean Annual Precipitation
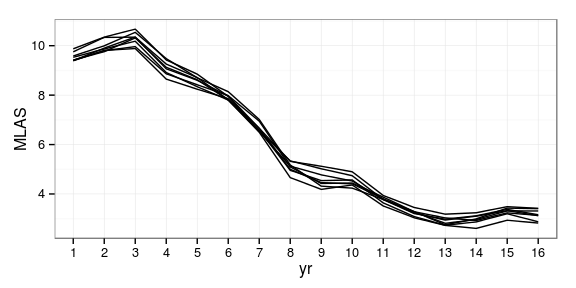
Mean response evolution by replicate
- There is a strong temporal trend that needs to be accounted for
Legendre Polynomials
- Family of orthogonal polynomials dense in \(\mathscr{L}_2\)
- Any regular curve can be approximated as much as needed by taking a linear combination of polynomials up to a high-enough order

Random-Regression model
\[ \begin{aligned} y_{ij} = & \mathrm{X}_i \beta + \Sigma_{k = 0}^{\mathrm{ord}} a_{ik} \mathcal{L}_k(j) + \varepsilon_{ij} \\ [a_0', \ldots, a_{\mathrm{ord}}']' \sim & N(0, \Sigma_{\mathrm{ord}} \otimes \mathrm{A})\\ \varepsilon \sim & N(0, \sigma_e^2) \end{aligned} \]
The Breeding Value of an individual is a function of an environmental variable (temp., precip., …)
This function is parameterised as a linear combination of Legendre orthogonal polynomials of order up to a given
orderEach individual is described by
order+ 1 coefficients
Example
- Functional Breeding Values for each individual